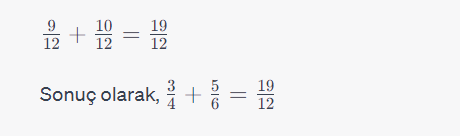Rasyonel Sayılar Konu Anlatımı PDF – Örnek Soru Çözümleri

Rasyonel Sayılar Konu Anlatımı PDF – Örnek Soru Çözümleri. Matematik konuları içerisinde yer alan Rasyonel sayılar özellikle sayısal problemlerin çözümünde önemli bir rol oynarlar. Bu makalemizde YKS-TYT-AYT Rasyonel sayılar konu anlatımı + PDF dosyası şeklinde anlatmaya çalıştık.
Rasyonel Sayılar Konu Anlatımı + PDF

Rasyonel sayı, bir tam sayının ya da iki tam sayının oranı şeklinde ifade edilebilen bir sayıdır. Yani bir rasyonel sayı, a/b şeklinde yazılabilir, burada a ve b tam sayıdır ve b sıfırdan farklıdır.
‘a/b’ rasyonel sayısında ‘a’ ya pay ‘b’ ye payda denir.
Örneğin, 3/4, -5/2, 0.6, 1 gibi sayılar rasyonel sayılardır çünkü her biri iki tam sayının oranı olarak ifade edilebilir. Ancak, √2 gibi bir sayı rasyonel değildir çünkü bu sayı iki tam sayının oranı olarak ifade edilemez.
Rasyonel sayılar, iki tam sayının birbirine bölünmesiyle elde edilen kesirlerdir. Kesirlerin pay ve payda kısımları tam sayı olmak zorundadır.
Rasyonel sayılar, kesirler veya ondalık sayılar gibi bir tam sayı ve bir kesirin bölünmesi ile elde edilen sayılardır. Rasyonel sayılar, toplama ve çıkarma işlemleri için bir dizi kurala tabidir. İşte rasyonel sayılarda toplama ve çıkarma işlemleri hakkında bilmeniz gerekenler:
Rasyonel Sayılarda Toplama işlemi
Rasyonel sayıların toplama işlemini yapmak için, öncelikle paydaları eşitlemeliyiz. Sonrasında payları toplamak için, her bir kesrin payını, eşitlenen paydaya göre yeniden düzenlememiz gerekecek.
Burada, paydalar 4 ve 6 olarak farklıdır, ancak bu iki sayının en küçük ortak katı (EKOK) 12’dir. Bu nedenle, her iki kesrin payını da 12’ye eşitleyebiliriz:
Şimdi, eşitlenen paylar üzerinden toplama işlemi yapabiliriz:
Sonucumuz basit hale getirilemiyor, ancak gerekirse daha sonra basitleştirilebilir.
Not: Eğer kesirlerin paydası zaten aynı ise, payları toplamak için doğrudan payları toplayabiliriz.
Rasyonel Sayılarda Çıkarma İşlemi
Rasyonel sayılar, yani kesirler, toplama ve çıkarma işlemleri için özel bir dikkat gerektirir. Rasyonel sayıları çıkarma işlemi yaparken, ilk olarak paydaların eşitlenmesi gerekir. Bunun için, her iki rasyonel sayının pay ve paydaslarını da ortak bir paydaya çevirmeniz gerekiyor.
Örneğin, 3/4 – 1/3 işlemini ele alalım. İlk olarak, bu iki kesirin paydaslarının çarpımını bulmanız gerekiyor. 4 ve 3’ün ortak çarpımı olan 12’yi payda olarak kullanabilirsiniz.
3/4 = 9/12 1/3 = 4/12
Bu durumda, 3/4 – 1/3 = 9/12 – 4/12 = (9-4)/12 = 5/12 olacaktır.
Başka bir örnek olarak, 2/5 – 1/10 işlemini ele alalım. İlk olarak, paydaları ortak hale getirmek için 10 ile çarpabilirsiniz:
2/5 = 4/10 1/10 = 1/10
2/5 – 1/10 = 4/10 – 1/10 = 3/10 olacaktır.
Bu şekilde, rasyonel sayıları çıkarma işlemini yapabilirsiniz.
Rasyonel Sayılarda Çarpma İşlemi
Rasyonel sayılarda çarpma işlemi, iki veya daha fazla rasyonel sayıyı çarpma işlemidir. Rasyonel sayılar, bir tam sayının bir kesire bölünmesiyle elde edilen sayılardır. Bu nedenle, rasyonel sayılar da kesir şeklinde ifade edilirler.
Örneğin, 2/3 ve 4/5 rasyonel sayılarıdır. Bu iki rasyonel sayıyı çarpmak için, kesirleri çarparak işleme devam ederiz:
2/3 x 4/5 = (2×4) / (3×5) = 8/15
Sonuç olarak, 2/3 ve 4/5’in çarpımı 8/15’tir.
Bir diğer örnek:
5/6 x 2/7 = (5×2) / (6×7) = 10/42
10/42 kesrinin sadeleştirilmesi için 2’ye bölerek basitleştirebiliriz:
10/42 = (2×5) / (2×21) = 5/21
Sonuç olarak, 5/6 ve 2/7’in çarpımı 5/21’dir.
Rasyonel sayıları çarpmak için, kesirleri çarparak işlemi devam ettirin ve sonuçta elde edilen kesri basitleştirin.
Rasyonel Sayılarda Bölme İşlemi
Rasyonel sayılar, yani kesirler, bölme işleminin sıkça kullanıldığı matematiksel bir kavramdır. Rasyonel sayılarda bölme işlemi, çarpma işlemine dönüştürülebilir. Bunu yapmak için, bölme işlemi yapılacak olan kesirlerin terslerinin alınması gerekir. Yani, bölünen kesir alınır ve tersi alınarak çarpan kesir bulunur.
Örneğin, 3/4 ile 2/3 kesirlerinin bölümünü bulmak istediğimizi varsayalım. Bu işlemi yapmak için, 2/3’ün tersini alarak çarpma işlemine dönüştürmemiz gerekiyor. 2/3’ün tersi 3/2’dir, bu yüzden işlemimiz şu şekilde olur:
(3/4) / (2/3) = (3/4) * (3/2) = 9/8
Böylece, 3/4 ile 2/3 kesirlerinin bölümü 9/8 olarak bulunur.
Bir diğer örnek vermek gerekirse, (5/6) / (2/9) işlemini yapmak istediğimizi düşünelim. Burada, 2/9’un tersi 9/2’dir, bu yüzden işlemimiz şu şekilde olur:
(5/6) / (2/9) = (5/6) * (9/2) = 15/4
Böylece, (5/6) / (2/9) işleminin sonucu 15/4 olarak bulunur.
Özetle, rasyonel sayılarda bölme işlemi, çarpma işlemine dönüştürülerek yapılabilir. Bölünen kesir alınarak tersi alınır ve çarpan kesir olarak kullanılır.
Rasyonel Sayılarda İşlem Önceliği
Rasyonel sayılarda işlem önceliği, matematikteki temel kurallardan biridir ve çarpma ve bölme işlemlerinin toplama ve çıkarma işlemlerine göre öncelikli olarak yapılması anlamına gelir.
Bu kurala göre, işlemler soldan sağa doğru yapılmalıdır. İlk olarak, parantez içindeki işlemler yapılır, ardından çarpma ve bölme işlemleri yapılır ve en sonunda da toplama ve çıkarma işlemleri yapılır.
Örneğin, aşağıdaki işlemde, öncelikle parantez içindeki işlem yapılır, sonra çarpma işlemi yapılır ve en son toplama işlemi yapılır:
4 + 3 x (8 ÷ 4) = 4 + 3 x 2 = 4 + 6 = 10
Burada, parantez içindeki işlem öncelikli olarak yapılır, çarpma işlemi toplama işleminden önce yapılır.
Bu kurala uyulmaması durumunda farklı sonuçlar elde edilebilir. Örneğin, aşağıdaki örnekte çarpma işlemi toplama işleminden önce yapılırsa, farklı bir sonuç elde edilir:
4 + 3 x 8 ÷ 4 = 4 + 24 ÷ 4 = 4 + 6 = 10
Bu nedenle, rasyonel sayılarda işlem önceliği kuralına uyulması önemlidir.
Örnek Soru Çözümleri
Rasyonel sayılar konusunu daha iyi kavrayabilmek için bol bol soru çözmeniz gereklidir.
Örnek: 3/4 + 5/8 işleminin sonucu nedir?
Çözüm:
Bu işlemi yapmak için öncelikle paydaları eşit hale getirmemiz gerekiyor.
4 ve 8 sayılarının en küçük ortak katı 8’dir, bu nedenle her bir payı 8’e eşitleyebiliriz.
3/4 = 6/8 (3’ü 4’e bölmek yerine, 2’ye bölüp, 3’ü çarpıyoruz)
5/8 = 5/8 (zaten 8’e eşit)
Bu işlemin toplamı şu şekilde hesaplanır:
6/8 + 5/8 = (6+5)/8 = 11/8
Yani, 3/4 + 5/8 işleminin sonucu 11/8’dir.
Örnek: 7/9 – 2/3 işleminin sonucu nedir?
Çözüm:
Bu işlemi yapmak için öncelikle paydaları eşit hale getirmemiz gerekiyor.
9 ve 3 sayılarının en küçük ortak katı 9’dur, bu nedenle her bir payı 9’a eşitleyebiliriz.
7/9 = 7/9 (zaten 9’a eşit)
2/3 = 6/9 (2’yi 3’e bölmek yerine, 3’ü çarpıp 6’yı elde ediyoruz)
Bu işlemin farkı şu şekilde hesaplanır:
7/9 – 6/9 = (7-6)/9 = 1/9
Yani, 7/9 – 2/3 işleminin sonucu 1/9’dur.
Örnek: (1/3) / (2/5) işleminin sonucu nedir?
Çözüm:
Bu işlemi yapmak için, payı birbiriyle çarpmamız gerekiyor. Ancak, (1/3) / (2/5) ifadesi, (1/3) x (5/2) ifadesine eşittir.
1/3 x 5/2 = (1 x 5) / (3 x 2) = 5/6
Yani, (1/3) / (2/5) işleminin sonucu 5/6’dır.
Örnek: (-2/3) x (9/4) işleminin sonucu nedir?
Çözüm:
(-2/3) x (9/4) = (-2 x 9) / (3 x 4) = -18/12 = -3/2
Rasyonel Sayılar Konu Anlatımı PDF
İlginizi Çekebilir 👇
👉 10. Sınıf Matematik Konu Anlatımı PDF
👉 Öğrenci Gündemi’ ni İnstagram’dan Takip Etmek İçin Tıklayınız